在数学中，二次函数是一种基础而重要的函数形式，掌握二次函数图像的画法，不仅有助于理解函数的性质，还能为学习更复杂的函数图像打下坚实基础，本文将详细介绍二次函数图像的画法，包括确定函数类型、解析图像特征、标注关键信息等。

二次函数概述

二次函数是一种具有形式f(x) = ax² + bx + c（a ≠ 0）的函数，根据系数a、b、c的值，二次函数的图像可以表现为开口向上或向下的抛物线，掌握二次函数的基本形式及其性质，是绘制二次函数图像的基础。

二次函数图像的画法

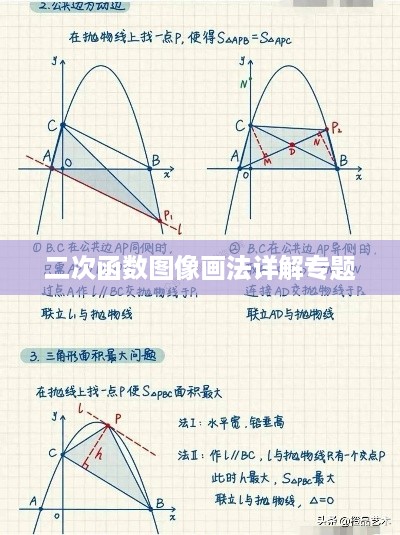
1、确定函数类型：根据二次函数的系数a的值，判断抛物线开口方向，当a > 0时，抛物线开口向上；当a < 0时，抛物线开口向下。

2、解析图像特征：根据二次函数的顶点公式（-b/2a, f(-b/2a)），找出抛物线的顶点，分析对称轴（x = -b/2a），理解抛物线的对称性。

3、标注关键信息：在图像上标注出与x轴的交点（即解方程f(x) = 0得到的根），以及函数的最大值或最小值点（即顶点），这些点是理解函数图像特征的关键。

4、绘制图像：根据以上信息，绘制出二次函数的图像，注意图像的平滑度和准确性。

实例分析

以二次函数f(x) = x² - 4x + 3为例，分析图像画法，确定函数类型，由于a = 1 > 0，抛物线开口向上，解析图像特征，根据顶点公式得到顶点为(2, -1)，标注关键信息，解方程f(x) = 0得到与x轴的交点为(1, 0)和(3, 0)，根据这些信息绘制出函数的图像。

注意事项

1、准确性：在绘制二次函数图像时，要确保计算的准确性，特别是顶点和与x轴的交点的位置。

2、平滑度：绘制图像时，要注意曲线的平滑度，以体现函数的连续性。

3、理解性质：理解二次函数的性质（如开口方向、对称轴、顶点等），有助于更准确地绘制图像。

本文详细介绍了二次函数图像的画法，包括确定函数类型、解析图像特征、标注关键信息等，通过实例分析，展示了具体的操作步骤，掌握二次函数图像的画法，有助于理解函数的性质，为学习更复杂的函数图像打下坚实基础，在绘制过程中，要注意准确性、平滑度以及对函数性质的理解。

拓展学习

学习完二次函数的图像画法后，还可以进一步拓展学习，如探讨不同形式的二次函数（如顶点式、交点式等）、研究二次函数的实际应用（如物理中的抛体运动、经济中的利润最大化问题等），通过拓展学习，可以更加深入地理解二次函数的知识。