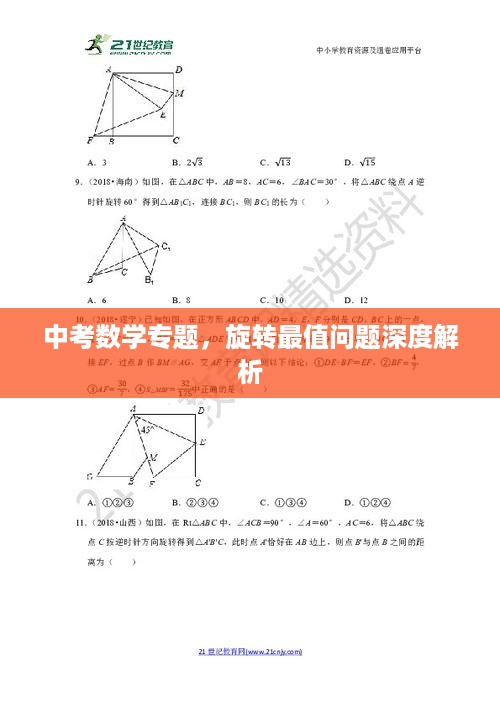
中考数学中，旋转最值问题是一个重要且具有一定难度的专题，这类问题主要考察学生的空间想象能力、数学逻辑思维以及解题策略，本文将详细解析旋转最值问题的常见类型、解题技巧以及应对策略，帮助考生更好地理解和掌握这一专题。

旋转最值问题的常见类型

1、旋转矩形最值问题：给定一个矩形，通过旋转求其周长或面积的最大值或最小值。

2、旋转三角形最值问题：涉及三角形的旋转，求相关线段长度、角度或面积的最大值或最小值。

3、立体图形旋转最值问题：在三维空间中，通过旋转立体图形求某些参数的最值。

解题技巧与策略

1、建立坐标系：对于涉及平面图形的旋转问题，建立适当的坐标系有助于简化问题，常用的坐标系有直角坐标系和极坐标系。

2、利用三角函数：旋转问题中，常常需要利用三角函数来求解角度、距离等参数。

3、转化法：将旋转问题转化为熟悉的数学问题，如二次函数、一元函数等，然后利用相关性质求解。

4、枚举法：对于一些特定的问题，可以通过枚举所有可能的情况来找到最值。

5、图解法：通过绘制图形，直观地观察最值的可能位置，有助于找到解题突破口。

典型例题解析

1、旋转矩形最值问题

例1：给定一个边长为a的等边三角形，将其绕一边的中点旋转60°，求旋转后三角形面积的最大值。

解析：首先建立直角坐标系，利用三角函数表示出旋转后的顶点坐标，根据三角形面积公式求出面积表达式，最后利用二次函数的性质求出面积的最大值。

2、旋转三角形最值问题

例2：给定一个直角三角形ABC，绕直角顶点C旋转，求旋转过程中线段AB的最大长度。

解析：通过枚举法，分析AB长度的变化情况，找到使其取得最大值的旋转角度，然后利用余弦定理等数学知识求出最大值。

复习建议与注意事项

1、掌握基础知识：熟练掌握三角函数、二次函数等基础知识，这是解决旋转最值问题的关键。

2、加强练习：通过大量练习，熟悉各类题型和解题技巧。

3、培养空间想象力：空间想象力是解决旋转最值问题的核心能力之一，平时可以通过立体图形、三维建模等方式进行训练。

4、注意题目中的陷阱：一些题目可能会设置陷阱，考生需要仔细阅读题目，避免掉入陷阱。

5、总结归纳：在解题过程中，及时总结归纳解题技巧和方法，形成自己的解题体系。

中考数学中的旋转最值问题是一个重要且具有一定难度的专题，考生需要掌握基础知识，加强练习，培养空间想象力，并注意题目中的陷阱，通过本文的解析和例题讲解，希望考生能够更好地理解和掌握这一专题，为中考取得好成绩打下坚实的基础。