什么是规范型矩阵形式

规范型矩阵形式是线性代数中的一个重要概念，它指的是一个矩阵经过一系列行变换和列变换后，最终达到的一种特定形式。这种形式对于解决线性方程组、矩阵的特征值和特征向量问题以及矩阵的秩等问题具有重要意义。规范型矩阵形式主要有两种：行规范型矩阵和列规范型矩阵。

行规范型矩阵

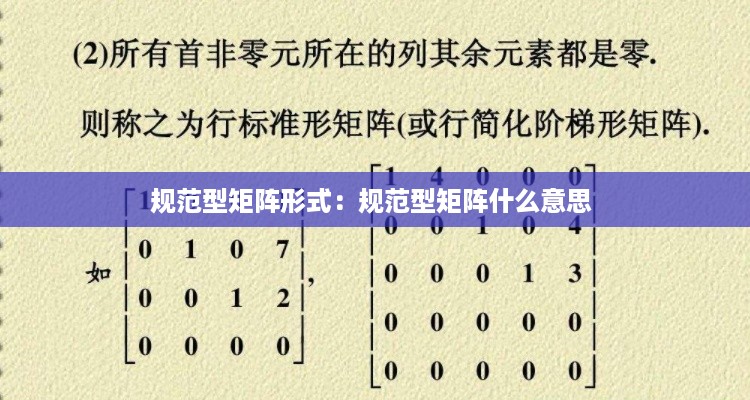
行规范型矩阵，也称为行最简形矩阵，是指一个矩阵经过行变换后，每一行的第一个非零元素（称为主元）都是1，且每个主元所在列的其他元素都是0。行规范型矩阵具有以下特点：

• 每行只有一个主元。
• 主元位于该行的最左侧。
• 主元所在列的其他行元素都是0。

行规范型矩阵对于解线性方程组非常重要，因为它可以帮助我们快速判断方程组是否有解以及解的唯一性。

列规范型矩阵

列规范型矩阵，也称为列最简形矩阵，是指一个矩阵经过列变换后，每一列的第一个非零元素（称为主元）都是1，且每个主元所在行的其他元素都是0。列规范型矩阵具有以下特点：

• 每列只有一个主元。
• 主元位于该列的最上方。
• 主元所在行的其他列元素都是0。

列规范型矩阵在解决线性方程组、矩阵的秩以及矩阵的相似问题等方面有着重要作用。

矩阵变换到规范型

要将一个矩阵变换到规范型，我们需要进行一系列的行变换和列变换。以下是一些常见的行变换和列变换方法：

• 行变换：
• 交换两行。
• 将一行乘以一个非零常数。
• 将一行加上另一行的倍数。
• 列变换：
• 交换两列。
• 将一列乘以一个非零常数。
• 将一列加上另一列的倍数。

通过这些变换，我们可以逐步将矩阵转换成行规范型或列规范型矩阵。

规范型矩阵的应用

规范型矩阵在数学和工程学等领域有着广泛的应用，以下是一些常见的应用场景：

• 解线性方程组：通过将方程组系数矩阵转换为行规范型矩阵，可以快速判断方程组是否有解以及解的唯一性。
• 矩阵的秩：通过将矩阵转换为行规范型矩阵，可以直观地看出矩阵的秩。
• 矩阵的相似性：两个矩阵如果可以通过一系列的行变换和列变换互相转换到规范型，则这两个矩阵是相似的。
• 矩阵的特征值和特征向量：通过将矩阵转换为对角矩阵或上三角矩阵，可以方便地求出矩阵的特征值和特征向量。

总之，规范型矩阵形式是线性代数中一个非常重要的概念，它在解决各种数学和工程问题中发挥着关键作用。

总结

规范型矩阵形式是线性代数中的一个基础概念，它通过行变换和列变换将矩阵转换成特定的形式，从而简化了线性方程组、矩阵的秩和特征值等问题。掌握规范型矩阵的相关知识对于学习线性代数和解决实际问题具有重要意义。