什么是高效优先队列

高效优先队列（High-Performance Priority Queue）是一种数据结构，它能够在对元素进行插入、删除和查找操作时保持高效性能。在计算机科学中，优先队列是一种抽象数据类型，它允许以某种排序方式存储元素，其中每个元素都有一个优先级。在高效优先队列中，元素总是按照优先级从高到低（或从低到高）排列。这种数据结构在许多应用场景中都非常有用，比如任务调度、实时系统、图算法等。

优先队列的基本操作

优先队列通常支持以下基本操作：

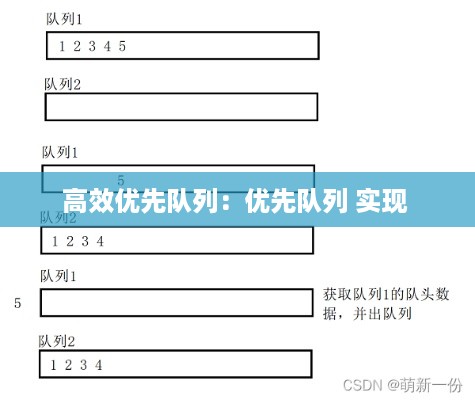
• 插入（Insert）：将一个新元素插入到队列中，并根据其优先级确定其在队列中的位置。
• 删除（Delete）：移除并返回优先级最高的元素。
• 最小（Min）或最大（Max）：返回优先级最高（或最低）的元素，但不从队列中移除。
• 检查（Check）：返回队列是否为空。

高效优先队列的关键在于能够快速找到并移除优先级最高的元素，这是通过底层数据结构的设计来实现的。

高效优先队列的底层数据结构

高效优先队列通常使用以下几种底层数据结构之一来实现：

• 堆（Heap）：堆是一种二叉树，其中每个父节点的值都小于或等于其子节点的值（最小堆）或大于或等于其子节点的值（最大堆）。堆可以快速地找到并删除最大（或最小）元素。
• 斐波那契堆（Fibonacci Heap）：斐波那契堆是一种基于链表的堆，它提供了一种更有效的方式来插入和合并堆，特别适合于动态环境中频繁的插入和删除操作。
• 二叉搜索树（BST）：虽然BST的查找、插入和删除操作的时间复杂度在最坏情况下可以达到O(n)，但在平均情况下，特别是当树是平衡的时候，BST可以提供高效的性能。

堆和斐波那契堆是优先队列中最常用的数据结构，因为它们能够提供接近O(log n)的插入和删除操作的时间复杂度。

堆的实现

堆的实现通常涉及到以下步骤：

• 创建一个数组来存储堆的元素。
• 定义一个堆调整（Heapify）过程，它确保在插入或删除元素后堆的性质得到维护。
• 实现插入（Insert）操作，它将新元素添加到数组的末尾，然后通过堆调整过程调整堆的结构。
• 实现删除（Delete）操作，它删除堆顶元素，然后将最后一个元素移动到堆顶，然后再次通过堆调整过程调整堆的结构。

最小堆的实现较为简单，而最大堆的实现需要稍微复杂一些，通常是通过最小堆实现后再取元素的反转来得到。

斐波那契堆的优势

斐波那契堆在以下方面优于传统堆：

• 插入操作的时间复杂度接近O(1)，而传统堆的插入操作时间复杂度为O(log n)。
• 合并操作的时间复杂度为O(1)，而传统堆的合并操作时间复杂度为O(n)。
• 对于某些特定的应用场景，斐波那契堆可以提供更好的性能。

然而，斐波那契堆的缺点是它比传统堆更复杂，且在空间复杂度上略高。

总结

高效优先队列是一种强大的数据结构，它能够在各种应用场景中提供高效的性能。通过使用合适的底层数据结构，如堆或斐波那契堆，我们可以确保优先队列的操作能够快速执行。选择合适的优先队列对于实现高性能算法至关重要，尤其是在需要频繁进行插入、删除和查找操作的情况下。